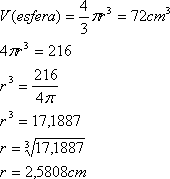Monomios: suma, resta, multiplicación, división y potencia

Nuevo vídeo-clase de Álgebra: Monomios y operaciones con monomios ;-)

Monomios: suma, resta, multiplicación, división y potencia

Área y perímetro cuadrado y triángulo:superficie semejante. Geometría ES...

Área y perímetro rectángulo, con ecuación segundo grado. Geometría ESO b...

Calcular área y perímetro cuadrado y triángulo: superficies semejantes - Nivel ESO

Calcular área y perímetro cuadrado y triángulo: superficies semejantes - Nivel ESO

Enésima configuración de triángulos de cerillas-fósforos

a) La configuración 1 está formada por 3 cerillas, la 2 lo está por 9 cerillas, etc. Mediante una búsqueda inductiva, determina cuál es el número de cerillas que tendrá la configuración número 12, si se mantiene el mismo criterio de construcción. 

 b) ¿Por cuántas cerillas estará constituida la enésima configuración?

SOLUCIÓN:

a) Tenemos varias configuraciones formadas por triángulos equiláteros cuyos lados son fósforos. Observamos que conforme aumenta el número de lados de los triángulos el número de fósforos que componen la figura crece. Realicemos una tabla de los 4 primeros casos para intentar encontrar alguna “regularidad”.

Lados	Nº triángulos	Fósforos por triángulo	Fósforos total configuración
1	1	X3	3
2	3	X3	9
3	6	X3	18
4	10	X3	30

Observamos cómo cada configuración nos da una cantidad distinta de triángulos, para obtener los fósforos totales basta con multiplicar por 3 (fósforos que tiene cada triángulo) por el número de triángulos que obtenemos.

Sin necesidad de dibujar el resto de configuraciones hasta la número 12, podemos completar la tabla hasta la doceava configuración si seguimos los criterios de construcción que se pueden observar en la tabla anterior. Un criterio puede ser que si sumamos al número de triángulos de la configuración n=1 el valor del siguiente n, es decir 2, obtenemos el número de triángulos para la configuración 2, que es 3, si al número de triángulos que tiene la configuración n=2, que son 3 triángulos, sumamos el valor de la siguiente configuración que es n=3, nos da 6, que es el número de triángulos de la configuración n=3, y así sucesivamente hasta llegar a n=12. 

Completemos la tabla hasta obtener el número de fósforos para la configuración de 12 lados, bastará con multiplicar por 3 el número de triángulos que tenga esa configuración. 

Lados	Nº triángulos	Fósforos por triángulo	Fósforos total configuración
1	1	X3	3
2	3	X3	9
3	6	X3	18
4	10	X3	30
5	15	X3	45
6	21	X3	63
7	28	X3	84
8	36	X3	108
9	45	X3	135
10	55	X3	165
11	66	X3	198
12	78	X3	234

Por lo tanto, el número de fósforos que tendrá la configuración nº 12 es de 234.

b) ¿Por cuántas cerillas estará constituida la enésima configuración?

Para hallar esta regularidad nos hemos tenido que dar cuenta antes de que el número de triángulos va creciendo conforme a la suma de las configuraciones n, es decir, estamos ante la suma de los “n” primeros números naturales, y esto nos facilita mucho las cosas...

Si deseamos obtener la suma de los n primeros números naturales tenemos que sumar término a término la expresión de dicha suma pero escrita en el orden opuesto, así:

S(n)=1+2+3+… +(n-2)+(n-1)+n

S(n)=n+(n-1)+(n-2)+… +3+2+1

2S(n)=n+1+(n-1)+2+(n-2)+3+… +3+(n-2)+2+(n-1)+1+n

2S(n)=(n+1)+(n+1)+(n+1)+… +(n+1)+(n+1)+(n+1)

Dado que, lógicamente, el sumando (n+1) se repite n veces, tenemos que:

2S(n)=n(n+1)

Despejando S(n) nos da:

Que es la expresión que nos indica la suma de los n primeros números naturales.

En nuestro ejercicio, dicha suma coincide con el número de triángulos de cada configuración; como cada triángulo tiene 3 fósforos (no olvidemos que nos piden el número de cerillas para la enésima configuración), bastará con multiplicar dicha expresión por 3, de este modo:

Comprobamos que para n=12 lados obtenemos el mismo resultado que mediante la anterior tabla de la búsqueda inductiva del punto a):

Demostración de J.A. Garfield del TEOREMA DE PITÁGORAS

MODELO VISUAL GEOMÉTRICO (TEOREMA DE PITÁGORAS)

Explicación de cómo se puede demostrar el teorema de Pitágoras a partir del modelo visual de la figura indicada, debido a J. A. Garfield (1876), que fue Presidente de los Estados Unidos de América.

 

 Garfield giró +90º un triángulo rectángulo en el sentido de las agujas del reloj y de centro el vértice de ángulo menor, como indicamos a continuación:

A este triángulo fruto del giro del original le aplicó una traslación de vector la hipotenusa del primer triángulo, de esta forma:

Uniendo los dos vértices obtuvo un trapecio rectángulo como el del siguiente dibujo:

Garfield calculó, primeramente, el área del trapecio resultante mediante la conocida fórmula del área del trapecio 

=

 

Después, Garfield calculó el área de cada uno de los 3 triángulos que componen el trapecio de la figura, mediante la conocida fórmula del área de un triángulo 

Siendo “c” la hipotenusa de cada uno de los 2 triángulos rectángulos que forman el trapecio.

Posteriormente, sumó las 3 áreas con la intención de obtener el área total del trapecio, que está compuesto por los 3 triángulos, así:

 Nota: el 2/2 se va y nos queda

Para terminar, si igualamos el área del trapecio obtenida mediante su fórmula correspondiente, y ésta última obtenida mediante la suma de las áreas de los 3 triángulos que componen el trapecio, obtenemos lo siguiente:

¡¡OBTENEMOS  LA EXPRESIÓN DEL TEOREMA DE PITÁGORAS¡¡ ;-)

El cuadrado de la hipotenusa (c) es igual a la suma del cuadrado de los catetos (a y b).

Razón Áurea o Número de Oro. Construye gráficamente un rectángulo áureo a partir de un cuadrado de lado 8 cm.

RAZÓN ÁUREA. RECTÁNGULO ÁUREO. Construye gráficamente un rectángulo áureo a partir de un cuadrado de lado 8 cm. ¿Cuáles son sus dimensiones? Comprueba que el rectángulo construido es áureo. Determina, en mm², la superficie del citado rectángulo.

El rectángulo áureo aparece con frecuencia en la naturaleza, así como en muchas obras artísticas y objetos inventados por el hombre. Se le denomina también como rectángulo de oro, y es el rectángulo cuyos lados están en “razón áurea”. La razón áurea, o número de oro, es un número algebraico irracional (decimal infinito no periódico) que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción entre segmentos de rectas. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza. Puede hallarse en elementos geométricos, en las nervaduras de las hojas de algunos árboles, en el grosor de las ramas, en el caparazón de un caracol, en los flósculos de los girasoles, etc.

Asimismo, se atribuye un carácter estético a los objetos cuyas medidas guardan la proporción áurea. A lo largo de la historia, se ha atribuido su inclusión en el diseño de diversas obras de arquitectura y otras artes.

El número áureo es el valor numérico de la proporción que guardan entre sí dos segmentos de recta a y b que cumplen la siguiente relación:

Este valor numérico nos debe arrojar el siguiente resultado:

 

 La actividad nos pide que construyamos gráficamente un rectángulo áureo a partir de un cuadrado de 8 cm de lado. Para que ese rectángulo pueda ser considerado áureo se debe cumplir lo siguiente:

 

Siendo “a” el lado mayor del rectángulo y “b” el lado menor.

 

Vamos a construir nuestro rectángulo áureo utilizando el programa GeoGebra.

Primero, dibujamos un cuadrado ABCD de lado 8 cm.

Segundo, tomamos el punto medio del lado del cuadrado AB, a dicho punto medio lo llamamos E y lo unimos, mediante un segmento al vértice C.

 

 

Tercero, con radio EC (valor 8,94) y centro en E, trazamos una circunferencia que corta a la recta horizontal en el punto F (valor 12,94)

 

Cuarto, unimos F con G y con C y se obtiene el rectángulo áureo ABGF:

Gracias al programa Geogebra, podemos hallar rápidamente las medidas y dimensiones de nuestro rectángulo áureo.

-          Lado AF y DG = 12,94 cm

-          Lado AD y FG = 8 cm

-          Área del rectángulo: base x altura = 12,94 x 8 = 103,52 cm²

-          Superficie del rectángulo en mm²: 10352 mm²

Vamos a comprobar que nuestro rectángulo cumple con las medidas del rectángulo áureo:

¡¡¡¡NUESTRO NÚMERO DE ORO!!!! 

Esferas y cubo. Volúmen y área de esfera y cubo.

ESFERAS Y CUBO. Un niño construyó un cubo macizo de plastilina, de 6 cm de arista. Luego lo deformó y construyó, con toda la plastilina que componía el cubo, tres bolas esféricas macizas iguales. 

a) ¿Cuál es el radio, en mm, de cada una de las bolas?

b) ¿Cuál es la superficie, en dm², de cada una de las bolas?

    Representa gráficamente tanto el cubo como las bolas.

Representamos, en primer lugar, y mediante el programa Cabri 3D, el cubo de arista 6 cm que construyó el niño.

Para averiguar la cantidad de plastilina que utilizó el niño para realizar este cubo macizo debemos hallar el volumen del mismo, como conocemos la arista a=6cm, sólo tenemos que emplear la fórmula del volumen del hexaedro regular o cubo.

Esta cantidad de plastilina la dividió en 3 bolas esféricas macizas iguales, por lo que el volumen de cada una de las esferas es de 216:3 = 72cm³

Conociendo el dato del volumen de las esferas macizas es muy fácil obtener el radio, en mm, de cada una de las bolas, que es lo que nos pide el ejercicio en su punto a). Podemos despejar el radio ( r ) de la fórmula del volumen de la esfera, de esta forma:

Como el radio nos lo pide en mm, basta con multiplicar por 10 el resultado obtenido en cm.

r = 2,5808cm x 10 = 25,808 mm

También podríamos haber hallado directamente el radio en mm si hubiéramos pasado el volumen de cm cúbicos a mm cúbicos. ¿Lo hacemos? ¡Adelante! Los cm³ se pasan a mm³ multiplicando por 1000, por lo que 72cm³=72000mm³

 

Una vez que conocemos el radio, r = 2,58 cm, podemos dibujar las 3 esferas con el Cabri 3D, quedando de esta forma:

Para terminar la actividad, y el plan completo por fin, nos piden que hallemos la superficie, en dm², de cada una de las bolas. Como son iguales, la superficie será la misma para cada una de ellas.

Como conocemos el radio r = 2,58 cm, podemos usar directamente la fórmula del área de la superficie esférica:

Como el ejercicio nos pide el área expresada en dm², tenemos que dividir la cantidad obtenida entre 100, así:

83,64cm² : 100 = 0,8364 dm²

También, podríamos haber hallado directamente el área en dm. cuadrados si hubiéramos expresado el radio en decímetros (2,58 cm = 0,258 dm) para hallar el área de la esfera, de este modo: